Vector bundle¶

This module implements algebraic algorithms for manipulating vector bundles as pairs of lattices over its function field. Follows the algorithmic methods discussed in [Mon24]

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: order = K.maximal_order()
sage: ideals = [K.places_finite()[0].prime_ideal()^-1, order.ideal(1)]
sage: g_finite = identity_matrix(K,2)
sage: g_infinite = matrix(K,[[1, 0], [0, 1/x^2*y]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite); V
Vector bundle of rank 2 over Function field in y defined by y^2 + 2*x^3 + 2*x

We can compute a basis of the space of global sections of V:

sage: h0 = V.h0(); h0
[(1, 0)]

We can also compute a basis of the 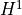$H^1$ group of V. First, a basis of its dual is computed:

sage: h1_dual, _ = V.h1_dual(); h1_dual
[[0 1]]

Then, we compute a representent of a linear form over h1_dual:

sage: V.h1_element([1])
[0, (x/(x^2 + 1))*y]

We can verify the Riemann-Roch theorem:

sage: len(h0) - len(h1_dual) == V.degree() + V.rank()*(1 - K.genus())
True

REFERENCES:

[At57]

M. F. Atiyah Vector Bundles on Elliptic Curves Proc. Lond. Math. Soc. 3(1):414-452, 1957

[Mon24]

M. Montessinos Algebraic algorithms for vector bundles over algebraic curves In preparation

[Sav08]

V. Savin Algebraic-Geometric Codes from Vector Bundles and their Decoding

[NR69]

M. S. Narasimhan and S. Ramanan Moduli of vector bundles on a compact Riemann surface Ann. of Math. 89(1):14-51, 1969

AUTHORS:

_Mickaël Montessinos: initial implementation

class vector_bundle.vector_bundle.VectorBundle(function_field, ideals, g_finite=None, g_infinite=None, check=True)¶

Bases: SageObject

A vector bundle defined over a normal curve with function field K.

If g_finite and g_infinite are None and ideals is a divisor, the line bundle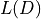 $L(D)$ is returned.

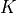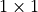If the constructed vector bundle is to have rank one, ideals may be an ideal instead of a list. Likewise, g_finite and g_infinite can be elements of $K$ rather that matrices of size $1 \times 1$ .

INPUT:

function_field – FunctionField; the function field of the bundle
ideals – list of coefficient ideals of the finite part of the bundle
g_finite – matrix; a basis of the finite part of the bundle
g_infinite – matrix; a basis of the infinite part of the bundle

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: VectorBundle(F,x.poles()[0].divisor())
Vector bundle of rank 1 over Rational function field in x over Finite Field of size 3
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [y, 2]])
sage: g_infinite = matrix([[x, y], [x + y, 1]])
sage: VectorBundle(K, ideals, g_finite, g_infinite)
Vector bundle of rank 2 over Function field in y defined by y^2 + 2*x^3 + 2*x

A line bundle may be defined without using lists and matrices:

sage: VectorBundle(K, K.maximal_order().ideal(1), 1, 1)
Vector bundle of rank 1 over Function field in y defined by y^2 + 2*x^3 + 2*x

It may also be defined using a divisor:

sage: VectorBundle(K, K.one().divisor())
Vector bundle of rank 1 over Function field in y defined by y^2 + 2*x^3 + 2*x

apply_isomorphism(isom)¶

Isom is an invertible square matrix of order self.rank(). Return the image of self by isom.

EXAMPLES

sage: from vector_bundle import (trivial_bundle, canonical_bundle,
....:                            atiyah_bundle)
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: triv = trivial_bundle(K)
sage: can = canonical_bundle(K)
sage: iso = triv.isomorphism_to(can)
sage: triv.hom(can).is_isomorphism(iso)
True
sage: V = can.direct_sum(atiyah_bundle(K, 2, 0, can))\
....:     .direct_sum(triv)
sage: W = can.direct_sum(atiyah_bundle(K, 2, 0)).direct_sum(can)
sage: iso = V.isomorphism_to(W)
sage: V.apply_isomorphism(iso) == W
True

basis_finite()¶

Return the basis vectors of the finite part of self.

The basis elements may not be in the corresponding lattice over the finite maximal order: the lattice may not be free and one must account for the coefficient ideals.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: V.basis_finite()
[(1, 2), (x, y)]

basis_infinite()¶

Return the basis vectors of the infinite part of self.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: V.basis_infinite()
[(x, 2), (1, y)]

basis_local(place)¶

Return a local basis of self at prime.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: V.basis_local(K.places_finite()[0])
[(x, 2*x), (x, y)]

coefficient_ideals()¶

Return the coefficient ideals of the finite part of self.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: Is = V.coefficient_ideals()
sage: Is == [P.prime_ideal() for P in K.places_finite()[:2]]
True

conorm(K)¶

Return the conorm of the vector bundle over an extension of its base

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in F.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, x]])
sage: g_infinite = matrix([[x, 1], [2, x]])
sage: V = VectorBundle(F, ideals, g_finite, g_infinite)
sage: VK = V.conorm(K)
sage: VK.rank()
2
sage: VK.degree() == K.degree() * V.degree()
True

coordinates_in_h0(f, check=True)¶

Return a vector of coordinates of f in the basis returned by self.h0()

If check is True, it is check whether f actually lies in the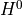 $H^0$ space, and None is output if f is not in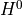 $H^0$ . If check is set to False the result may be garbage.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(7))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1,1 / (x**5 + y)],[2, y]])
sage: g_infinite = matrix([[x, 1], [2, y**3]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: h0 = V.h0()
sage: v = sum([i*e for i, e in enumerate(h0)])
sage: V.coordinates_in_h0(v)
(0, 1, 2, 3, 4, 5)

degree()¶

Returns the degree of the vector bundle.

This is defined as the degree of the divisor of the determinant bundle.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: V.degree()
-1

determinant¶

File: /home/mickael/Math/Code/Published/vector_bundles/vector_bundle/vector_bundle.py (starting at line 357)

Return the determinant bundle.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: d = V.determinant()
sage: d._ideals
[Ideal (x) of Maximal order of Function field in y defined by y^2 + x + 2]
sage: d._g_finite
[y + x]
sage: d._g_infinite
[x*y + 1]

direct_sum(other)¶

Returns the direct sum of two vector bundles

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V1 = VectorBundle(K, ideals, g_finite, g_infinite)
sage: O = K.maximal_order()
sage: V2 = VectorBundle(K, O.ideal(1), 1, x^2)
sage: V = V1.direct_sum(V2)
sage: V.rank() == V1.rank() + V2.rank()
True
sage: V.degree() == V1.degree() + V2.degree()
True

direct_sum_repeat(n)¶

Return the direct sum of n copies of self.

EXAMPLES

sage: from vector_bundle import trivial_bundle
sage: F.<x> = FunctionField(GF(3))
sage: L = trivial_bundle(F)
sage: V = L.direct_sum_repeat(3)
sage: V.rank()
3
sage: V.degree()
0
sage: V.h0()
[(1, 0, 0), (0, 1, 0), (0, 0, 1)]

dual()¶

Returns the dual vector bundle of self.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: Vd = V.dual()
sage: Vd.rank() == V.rank()
True
sage: Vd.degree() == -V.degree()
True

end()¶

Return the hom bundle of endomorphisms of self.

Examples

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: L1 = VectorBundle(F, x.zeros()[0].divisor())
sage: L2 = VectorBundle(F, x.poles()[0].divisor())
sage: E = L1.direct_sum(L2).end(); E.h0()
[
[1 0]  [0 0]  [  0 1/x]  [0 0]
[0 0], [x 0], [  0   0], [0 1]
]

extension_by_global_sections()¶

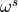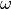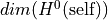Return the canonical extension of self by $\omega^s$ where $\omega$ is the canonical line bundle and $s$ is $dim(H^0(\mathrm{self}))$ .

This extension is defined in [At57] for elliptic curves, but the constructions generalises to arbitrary genus if one replaces the trivial line bundle with a canonical line bundle.

EXAMPLES

sage: from vector_bundle import trivial_bundle, VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: T = trivial_bundle(K)
sage: E = T.extension_by_global_sections()
sage: E.rank()
2
sage: E.end().h0()
[
[0 1]  [1 0]
[0 0], [0 1]
]
sage: L = VectorBundle(K,K.places_infinite()[0].divisor())
sage: E = (E.tensor_product(L)).extension_by_global_sections()
sage: E.rank()
4
sage: E.degree()
2
sage: E.hom(E).h0()
[
[0 1 0 0]  [1 0 0 0]
[0 0 0 0]  [0 1 0 0]
[0 0 0 1]  [0 0 1 0]
[0 0 0 0], [0 0 0 1]
]

extension_group¶

File: /home/mickael/Math/Code/Published/vector_bundles/vector_bundle/vector_bundle.py (starting at line 996)

Return the extension group of self by other. If precompute_basis is set to True, a basis of the extension group is precomputed. Extensions may be constructed without using a precomputed basis, but each construction is a bit costlier this way. You should precompute a basis if you are planning to compute an number of extensions larger than the dimension of the ext group.

EXAMPLES:

sage: from vector_bundle import trivial_bundle, canonical_bundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: trivial_bundle(K).extension_group(canonical_bundle(K))
Extension group of Vector bundle of rank 1 over Function field in 
y defined by y^2 + 2*x^3 + 2*x by Vector bundle of rank 1 over 
Function field in y defined by y^2 + 2*x^3 + 2*x.

function_field()¶

Return the function field of the vector bundle

EXAMPLES

sage: from vector_bundle import trivial_bundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: V = trivial_bundle(K)
sage: V.function_field()
Function field in y defined by y^2 + 2*x^3 + 2*x

h0()¶

Returns a basis of the 0th cohomology group of self

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1,1 / (x**5 + y)],[2, y]])
sage: g_infinite = matrix([[x, 1], [2, y**3]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: V.degree()
6
sage: h0 = V.h0(); len(h0)
6
sage: all([all([c in ideals[i] for i,c in enumerate(list(g_finite**-1 * v))]) for v in h0])
True
sage: O_infinity = K.maximal_order_infinite()
sage: all([all([c in O_infinity for c in g_infinite**-1 * v]) for v in h0])
True

TESTS

sage: from vector_bundle import VectorBundle
sage: from vector_bundle import canonical_bundle
sage: F.<x> = FunctionField(GF(3))
sage: ideals = [F.maximal_order().ideal(x), F.maximal_order().ideal(1 / (1+x^3))]
sage: g_finite = matrix([[x^-5, x^-1], [2 + x^-2, 1]])
sage: g_infinite = matrix([[2*x + x^-2, 2], [x^3 + 2*x^-1, 1]])
sage: V = VectorBundle(F, ideals, g_finite, g_infinite)
sage: V.degree()
6
sage: h0 = V.h0(); len(h0)
8
sage: all([all([c in ideals[i] for i,c in enumerate(list(g_finite**-1 * v))]) for v in h0])
True
sage: O_infinite = F.maximal_order_infinite()
sage: all([all([c in O_infinite for c in g_infinite**-1 * v]) for v in h0])
True
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^4 - x**-2 - 1)
sage: L = canonical_bundle(K)
sage: len(L.h0())
1

h0_from_vector(v)¶

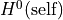Return an element of $H^0(\mathrm{self})$ from a vector of coordinates in the basis given by self.h0()

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(7))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1,1 / (x**5 + y)],[2, y]])
sage: g_infinite = matrix([[x, 1], [2, y**3]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: h0 = V.h0()
sage: v = vector(list(range(6)))
sage: V.coordinates_in_h0(V.h0_from_vector(v))
(0, 1, 2, 3, 4, 5)

h1_dimension()¶

Return the dimension of the 1st cohomology group of the vector bundle.

EXAMPLES

sage: from vector_bundle import trivial_bundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: L = trivial_bundle(K)
sage: L.h1_dimension()
1
sage: K.genus()
1

h1_dual¶

File: /home/mickael/Math/Code/Published/vector_bundles/vector_bundle/vector_bundle.py (starting at line 884)

Return the dual of the 1st cohomology group of the vector bundle. By Serre duality, this is the 0th cohomology group of canonical_bundle(self._function_field).tensor_product(self.dual())

OUTPUT:

a basis of the dual of the h1 of self
the hom bundle whose h0 has basis the first output

EXAMPLES

sage: from vector_bundle import trivial_bundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: L = trivial_bundle(K)
sage: L.h1_dual()
([[1]],
Homomorphism bundle from Vector bundle of rank 1 over Function field in y defined by y^2 + 2*x^3 + 2*x to Vector bundle of rank 1 over Function field in y defined by y^2 + 2*x^3 + 2*x)

h1_element(form=None)¶

Represent a linear form over self.h1_dual() under Serre duality.

INPUT:

form – vector of elements of self._function_field.constant_base_field() representing a linear form over self.h1_dual(). (default: [1,0,…,0])

OUTPUT:

‘’res’’ – vector of elements of K such that the corresponding infinite répartition vectorcorresponds to form under Serre duality with respect to safe_uniformizers(self._function_field)[0].differential().

EXAMPLES

sage: from vector_bundle import trivial_bundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: triv = trivial_bundle(K)
sage: triv.h1_element([1])
[(x/(x^2 + 1))*y]

hom(other)¶

Returns the hom bundle Hom(self,other)

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V1 = VectorBundle(K, ideals, g_finite, g_infinite)
sage: O = K.maximal_order()
sage: V2 = VectorBundle(K, O.ideal(1), 1, x^2)
sage: V = V1.hom(V2)
sage: V.rank() == V1.rank() * V2.rank()
True
sage: V.degree() == V2.degree()*V1.rank() - V1.degree()*V2.rank()
True

is_in_h0(v)¶

Check if vector v with coefficients in self.function_field() lies in the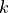 $k$ -vector space spanned by the output of self.h0()

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(7))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1,1 / (x**5 + y)],[2, y]])
sage: g_infinite = matrix([[x, 1], [2, y**3]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: V.is_in_h0(V.h0_from_vector(vector(list(range(6)))))
True
sage: V.is_in_h0(vector([x^i for i in range(6)]))
False

is_locally_trivial(place)¶

Check if the vector bundle is the trivial lattice at place place

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(7))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: L1 = VectorBundle(K, K.places_finite()[0].divisor())
sage: L2 = VectorBundle(K, K.places_finite()[1].divisor())
sage: V = L1.direct_sum(L2)
sage: V.is_locally_trivial(K.places_finite()[0])
False
sage: V.is_locally_trivial(K.places_finite()[2])
True
sage: V.is_locally_trivial(K.places_infinite()[0])
True
sage: L = VectorBundle(K,K.places_infinite()[0].divisor())
sage: L.is_locally_trivial(K.places_infinite()[0])
False

isomorphism_to(other)¶

Return an isomorphism from self to other if it exists and None otherwise

EXAMPLES

sage: from vector_bundle import (trivial_bundle, canonical_bundle,
....:                            atiyah_bundle)
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: triv = trivial_bundle(K)
sage: can = canonical_bundle(K)
sage: iso = triv.isomorphism_to(can)
sage: triv.hom(can).is_isomorphism(iso)
True
sage: V = can.direct_sum(atiyah_bundle(K, 2, 0, can))\
....:     .direct_sum(triv)
sage: W = can.direct_sum(atiyah_bundle(K, 2, 0)).direct_sum(can)
sage: iso = V.isomorphism_to(W)
sage: V.hom(W).is_isomorphism(iso)
True

WARNING:

Not well implemented for infinite fields: need to specify how to chose random elements and adequatly set the sample size.

non_trivial_extension(other)¶

Return any nontrivial extension of self by other.

EXAMPLES:

sage: from vector_bundle import trivial_bundle, canonical_bundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: triv = trivial_bundle(K)
sage: can = canonical_bundle(K)
sage: V = triv.non_trivial_extension(can)
sage: V.rank()
2
sage: V.degree()
0
sage: V.h0()
[(1, 0)]
sage: V.end().h0()
[
[0 1]  [1 0]
[0 0], [0 1]
]

rank()¶

Return the rank of a vector bundle.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: O = K.maximal_order()
sage: V = VectorBundle(K, O.ideal(1), x, y)
sage: V.rank()
1

restriction()¶

Return the Weil restriction of the vector bundle over the base field of self._function_field

As a vector bundle is seen as a pair of lattices, the Weil restriction of a bundle is the pair of lattices seen above the maximal orders of the base field. Equivalently, if the field extension K in L corresponds to a morphism of curves f from Y to X, the restriction is the direct image under f.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V = VectorBundle(K, ideals, g_finite, g_infinite)
sage: VF = V.restriction()
sage: VF._ideals
[Ideal (1) of Maximal order of Rational function field in x over Finite Field of size 3,
Ideal (1) of Maximal order of Rational function field in x over Finite Field of size 3,
Ideal (1) of Maximal order of Rational function field in x over Finite Field of size 3,
Ideal (1) of Maximal order of Rational function field in x over Finite Field of size 3]
sage: VF._g_finite
[      x       1     x^2     2*x]
[      0       1       0       x]
[    2*x       2       0 2*x + 1]
[      0       2       x       2]
sage: VF._g_infinite
[          x           0           1           0]
[          0           1           0         1/x]
[          2           0           0 (2*x + 1)/x]
[          0         2/x           1           0]

slope()¶

Return the slop of the vector bundle.

The slope is the ratio rank/degree

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: from vector_bundle import trivial_bundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2-x^3-x)
sage: E = VectorBundle(K, K.places_infinite()[0].divisor())
sage: V = E.non_trivial_extension(trivial_bundle(K))
sage: V.slope()
1/2

split()¶

Return a list of indecomposable bundles inds, a list of integers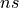 $ns$ and an isomorphism from $\bigoplus_{\mathrm{ind} \in \mathrm{inds}} \mathrm{ind}^{n_\mathrm{ind}}$ to self.

EXAMPLES:

sage: # long time (20 seconds)
sage: from vector_bundle import atiyah_bundle, trivial_bundle
sage: F.<x> = FunctionField(GF(7))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: triv = trivial_bundle(K)
sage: V = atiyah_bundle(K, 2, 0)
sage: W = triv.direct_sum_repeat(2).direct_sum(V)
sage: T = matrix(K, 4, 4,
....:            [x+1, 4, 3*x+4, 6*x+6,
....:             4*x+5, 6*x+5, 2*x+1, 4*x+3,
....:             3*x+1, 5*x, 3*x+1, x+6,
....:             5*x+4, 6*x, 5*x+2, 6*x+6])           
sage: W = W.apply_isomorphism(T)
sage: inds, ns, isom = W.split()
sage: b1 = [ind.rank() for ind in inds] == [1, 2]
sage: b2 = [ind.rank() for ind in inds] == [2, 1]
sage: b1 or b2
True
sage: b1 = ns == [1, 2]
sage: b2 = ns == [2, 1]
sage: b1 or b2
True
sage: sum = inds[0].direct_sum_repeat(ns[0])
sage: sum = sum.direct_sum(inds[1].direct_sum_repeat(ns[1]))
sage: sum.hom(W).is_isomorphism(isom)
True

tensor_power(n)¶

Return the n-th tensor power of self

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: L = VectorBundle(F, x.poles()[0].divisor())
sage: E = L.tensor_power(3)
sage: E.rank()
1
sage: E.degree()
3
sage: E.h0()
[(1), (x), (x^2), (x^3)]

tensor_product(other)¶

Returns the tensor product of two vector bundles

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 + x + 2)
sage: ideals = [P.prime_ideal() for P in K.places_finite()[:2]]
sage: g_finite = matrix([[1, x], [2, y]])
sage: g_infinite = matrix([[x, 1], [2, y]])
sage: V1 = VectorBundle(K, ideals, g_finite, g_infinite)
sage: O = K.maximal_order()
sage: V2 = VectorBundle(K, O.ideal(1), 1, x^2)
sage: V = V1.tensor_product(V2)
sage: V.rank() == V1.rank() * V2.rank()
True
sage: V.degree() == V1.degree()*V2.rank() + V2.degree()*V1.rank()
True

Vector bundle¶

Table of Contents

Previous topic

Next topic

This Page