Constructions¶
This module provides functions for various interesting constructions of vector bundles.
AUTHORS:
_Mickaël Montessinos: initial implementation
- vector_bundle.constructions.atiyah_bundle(field, rank, degree, base=None)¶
Return
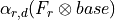 in the notation of Theorem 6 [At57]
, where
in the notation of Theorem 6 [At57]
, where  is
is rankand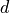 is
is degree.INPUT:
field- FunctionField; of genus 1 with an infinite place of degree 1rank- integerdegree- integerbase- line bundle of degree 0 over field ; (default =trivial_bundle(field))
EXAMPLES
sage: from vector_bundle import atiyah_bundle sage: from vector_bundle import VectorBundle sage: F.<x> = FunctionField(GF(11)) sage: R.<y> = F[] sage: K.<y> = F.extension(y^2 - x^3 - x) sage: base = VectorBundle( ....: K, ....: K.places_finite()[0].divisor() ....: - K.places_infinite()[0].divisor()) sage: E = atiyah_bundle(K, 5, 3, base) sage: E.rank() 5 sage: E.degree() 3 sage: E.hom(E).h0() [ [1 0 0 0 0] [0 1 0 0 0] [0 0 1 0 0] [0 0 0 1 0] [0 0 0 0 1] ]
- vector_bundle.constructions.canonical_bundle(K)¶
Return a canonical line bundle over K suitable for explicit Serre duality.
EXAMPLES
sage: from vector_bundle import canonical_bundle, trivial_bundle sage: F.<x> = FunctionField(GF(3)) sage: canonical_bundle(F).degree() -2 sage: R.<y> = F[] sage: K.<y> = F.extension(y^2 - x^3 - x) sage: L = canonical_bundle(K); L Vector bundle of rank 1 over Function field in y defined by y^2 + 2*x^3 + 2*x sage: L == trivial_bundle(K) True
- vector_bundle.constructions.rank_2_trivial_determinant_semistable_bundle(ksi, ext=None)¶
Construct the semi-stable vector bundle of rank 2 and trivial determinant defined by the extension of
ksibyksi.dual()and nonzero extension classext.The fact that this vector bundle is semi-stable is Lemma 5.1 in [NR69]. If
extis None, we default to a default nonzero extension class.INPUT:
ksi– a degree 1 line bundle over a function field of genus at least 2ext– an object representing a class of extensions ofksibyksi.dual(). (Default: None)
EXAMPLES
sage: from vector_bundle import VectorBundle, trivial_bundle, rank_2_trivial_determinant_semistable_bundle sage: F.<x> = FunctionField(GF(11)) sage: R.<y> = F[] sage: K.<y> = F.extension(y^2 - x^5 - 1) sage: ksi = VectorBundle(K, K.places_finite()[0].divisor()) sage: V = rank_2_trivial_determinant_semistable_bundle(ksi) sage: V.rank() 2 sage: V.determinant() == trivial_bundle(K) True
- vector_bundle.constructions.savin_bundle(field, rank, degree, line, line_1, line_2)¶
Return a weakly stable bundle over field of rank
rankand degreedegreeALGORITHM:
Section V of [Sav08]
INPUT:
field– FunctionField: the base of the bundle. Must have genus at least 2.rank– Integer: the rank of the output bundledegree– Integer: the degree of the output bundleline– VectorBundle: line bundle of degreedegree//rank + 1plays the role of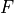 in the algorithm
in the algorithmline_1– VectorBundle: line bundle of degreedegree // rankplays the role of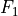 in the algorithm
in the algorithmline_2– VectorBundle: line bundle of degreedegree // rankplays the role of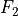 in the algorithm
in the algorithm
EXAMPLE
sage: from vector_bundle import VectorBundle, savin_bundle sage: F.<x> = FunctionField(GF(11)) sage: R.<y> = F[] sage: K.<y> = F.extension(y^2 - x^5 + x) sage: line = VectorBundle(K, 3 * K.places_infinite()[0].divisor()) sage: line_1 = VectorBundle(K, 2 * K.places_finite()[0].divisor()) sage: line_2 = VectorBundle(K, 2 * K.places_finite()[1].divisor()) sage: E = savin_bundle(K, 3, 7, line, line_1, line_2) sage: E.rank() 3 sage: E.degree() 7
- vector_bundle.constructions.trivial_bundle(K)¶
Return the structure sheaf of the algebraic curve with function field K.
EXAMPLES
sage: from vector_bundle import trivial_bundle sage: F.<x> = FunctionField(GF(3)) sage: R.<y> = F[] sage: K.<y> = F.extension(y^2 + x + 2) sage: O = K.maximal_order() sage: V = trivial_bundle(K) sage: V._ideals [Ideal (1) of Maximal order of Function field in y defined by y^2 + x + 2] sage: V._g_finite [1] sage: V._g_infinite [1]