Ext group

This module implements the ExtGroup and ExtGroupElement classes used for building extensions of vector bundles.

AUTHORS:

_Mickaël Montessinos: initial implementation

class vector_bundle.ext_group.ExtGroup(left, right, precompute_basis=False)

Bases: SageObject

The group of extensions of left by right.

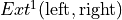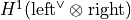The group Ext^1(\mathrm{left},\mathrm{right}) is H^1(\mathrm{left}^\vee \otimes \mathrm{right}). Its elements may be represented as matrices of infinite répartitions lying in M_{\mathrm{right}.rank(),\mathrm{left}.rank()}(R) or as vectors of length self.dim() with coefficients in the coefficient field, representing linear forms on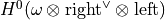 H^0(\omega \otimes \mathrm{right}^\vee \otimes \mathrm{left}), where 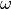\omega is the canonical bundle of the function field of left and right The two representations are related via Serre duality.

If precompute_basis is set to True, a basis of répartition matrices is computed. Its element represent the linear forms vector([0,...,0,1,0,...,0]). Otherwise, linear forms are converted to elements of the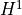 H^1 on the fly. You should set precompute_basis to True only if you plan to create several extensions with this group.

INPUT:

  • left – VectorBundle

  • right – VectorBundle; must have the same function field as left

  • precompute_basis – boolean

EXAMPLES

sage: from vector_bundle import VectorBundle, trivial_bundle
sage: F.<x> = FunctionField(GF(3))
sage: triv = trivial_bundle(F)
sage: triv.extension_group(triv)
Extension group of Vector bundle of rank 1 over Rational function field in x over Finite Field of size 3 by Vector bundle of rank 1 over Rational function field in x over Finite Field of size 3.
basis()

Return a basis of 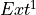Ext^1 group. Its element are matrices of infinite répartitions represented by field elements.

Computes and stores the basis if it was not precomputed yet.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(11))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^5 - 1)
sage: ksi = VectorBundle(K, K.places_finite()[0].divisor())
sage: ext = ksi.extension_group(ksi.dual()); ext.basis()
[[(x^9/(x^10 + 2*x^5 + 1))*y], [(x^3/(x^5 + 1))*y], [x^6/(x^5 + 1)]]
dim()

Return the dimension of the extension group as a vector space over the base coefficient field

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(11))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^5 - 1)
sage: ksi = VectorBundle(K, K.places_finite()[0].divisor())
sage: ext = ksi.extension_group(ksi.dual()); ext.dim()
3
dual_basis()

This is the same as self.dual_bundle().h0() The output basis is dual to self.basis() under Serre duality.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(11))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^5 - 1)
sage: ksi = VectorBundle(K, K.places_finite()[0].divisor())
sage: ext = ksi.extension_group(ksi.dual()); ext.dual_basis()
[[x^4/(x^5 + 6)], [x^5/(x^5 + 6)], [(x^2/(x^5 + 6))*y + 10*x^2/(x^5 + 6)]]
dual_bundle()

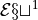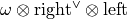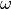Return the dual bundle of the \mathcal{Ext}^1 bundle. This bundle is \omega \otimes \mathrm{right}^\vee \otimes \mathrm{left}, where \omega is a canonical line bundle of K.

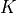EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(11))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^5 - 1)
sage: ksi = VectorBundle(K, K.places_finite()[0].divisor())
sage: ext = ksi.extension_group(ksi.dual()); ext.dual_bundle()
Homomorphism bundle from Vector bundle of rank 1 over Function 
field in y defined by y^2 + 10*x^5 + 10 to Vector bundle of rank 1
over Function field in y defined by y^2 + 10*x^5 + 10
extension(ext=None)

Return the extension of self.left() by self.right() encoded by ext.

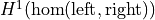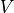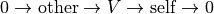
ext can be a matrix of elements of self._function_field which represents the constant value over the infinite places of a répartition matrix with support at infinity representing an element of H^1(\mathrm{hom}(\mathrm{left},\mathrm{right})). Such an element encodes an extension V: 0 \to \mathrm{other} \to V \to \mathrm{self} \to 0

ext can also be a vector of length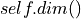 self.dim() representing an extension in the basis of the Ext vector space.

By default, ext is chosen as any non trivial extension.

EXAMPLES

sage: from vector_bundle import VectorBundle, trivial_bundle
sage: F.<x> = FunctionField(GF(11))
sage: R.<y> = F[]
sage: K.<y> = F.extension(y^2 - x^3 - x)
sage: triv = trivial_bundle(K)
sage: ext = triv.extension_group(triv)
sage: V = ext.extension()
sage: V.rank()
2
sage: V.determinant() == triv
True
sage: V.h0()
[(1, 0)]
sage: V.end().h0()
[
[0 1]  [1 0]
[0 0], [0 1]
]
left()

Return the left vector bundle of self.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: L1 = VectorBundle(F, x.zeros()[0].divisor())
sage: L2 = VectorBundle(F, x.poles()[0].divisor())
sage: ext = L1.extension_group(L2); ext.left() == L1
True
right()

Return the right vector bundle of self.

EXAMPLES

sage: from vector_bundle import VectorBundle
sage: F.<x> = FunctionField(GF(3))
sage: L1 = VectorBundle(F, x.zeros()[0].divisor())
sage: L2 = VectorBundle(F, x.poles()[0].divisor())
sage: ext = L1.extension_group(L2); ext.right() == L2
True